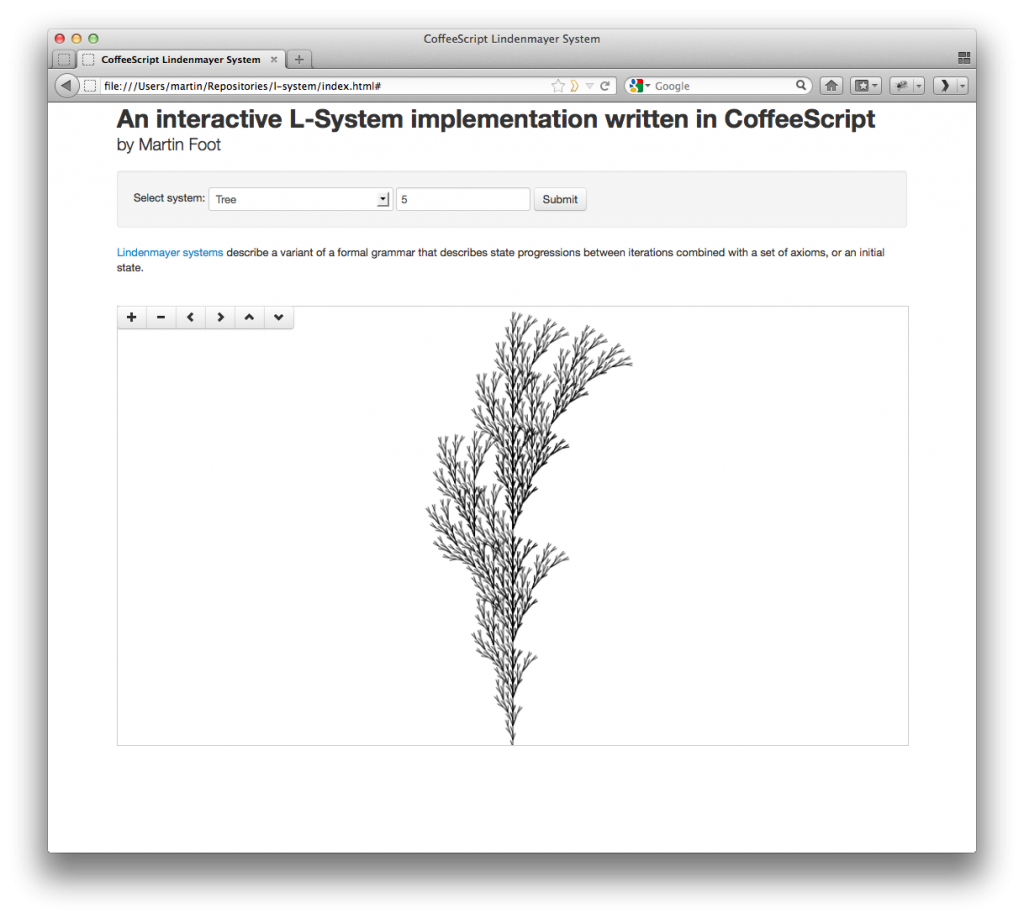
A Simple Lindenmayer System Renderer
I spent some time last week reading about Lindenmayer Systems (or L-Systems), then wrote a simple interactive L-System renderer in CoffeeScript that you can try out on GitHub.
L-Systems are a way of describing an image in terms of an axiom, a set of generation functions, and a set of rendering functions. They are represented as a string, and for each ‘generation’, the generation functions are applied to all symbols in that string to produce a new string. For example, given the axiom (starting truth) ‘A’ and the generation functions ‘A -> BA’, and ‘B -> AB’, generation one will be ‘BA’, then generation two will be ‘ABBA’.
We can then define a set of rendering functions that define what to draw when we reach each symbol such as ‘move forward 10 units’ and ‘turn left 20 degrees’. With each generation the system gets bigger and bigger, and it’s fantastic to play with.
For instance, the code below describes how to draw a Sierpinski Triangle using ‘turtle graphics’ and a simple stack:
'Sierpinski Triangle':
axiom: 'A'
rules:
'A': 'B-A-B'
'B': 'A+B+A'
renderFunctions:
'A': (stack) ->
turtle = stack.peek()
turtle.forward 10
'B': (stack) ->
turtle = stack.peek()
turtle.forward 10
'-': (stack) ->
turtle = stack.peek()
turtle.left 60
'+': (stack) ->
turtle = stack.peek()
turtle.right 60Which, when rendered for five generations looks like this:
 The source code for the render is available here.
The source code for the render is available here.